| (77) |
Now, we will consider a more interesting Ising system; namely, that of interacting spins on a 2d square lattice. What do we mean by interacting? We mean that the Hamiltonian depends on pairs of spins:
Think about this Hamiltonian. It says that energy is minimal when all
![]() spins have the same alignment, either all up or all down. Imagine
a microscopic observable called the magnetization, or average
spin orientation,
spins have the same alignment, either all up or all down. Imagine
a microscopic observable called the magnetization, or average
spin orientation, ![]() :
:
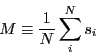 |
(78) |
Our physical intution tells us that as ![]() 0,
0,
![]() 1, and as
1, and as
![]() ,
,
![]() 0. The fascinating thing about an Ising
magnet is that there is a finite temperature called the critical
temperature,
0. The fascinating thing about an Ising
magnet is that there is a finite temperature called the critical
temperature, ![]() . If we start out with a ``hot'' system, and cool
it to just below
. If we start out with a ``hot'' system, and cool
it to just below ![]() , the absolute value of the magnetization
spontaneously jumps from 0 to some finite positive value. In other
words, the system undergoes a phase transition from a disordered
phase to a partially ordered phase. A Metropolis Monte Carlo
simulation can allow us to probe the behavior of an Ising system and
learn how the system behaves near criticality. The rest of this case
study will be devoted to showing you the inner workings of a C
program which simulates the Ising lattice using Metropolis MC, as a
first implementation of this technique. In the suggested exercises
appearing at the end of this case study, you will modify this code
slightly to compute averages values of certain observables.
, the absolute value of the magnetization
spontaneously jumps from 0 to some finite positive value. In other
words, the system undergoes a phase transition from a disordered
phase to a partially ordered phase. A Metropolis Monte Carlo
simulation can allow us to probe the behavior of an Ising system and
learn how the system behaves near criticality. The rest of this case
study will be devoted to showing you the inner workings of a C
program which simulates the Ising lattice using Metropolis MC, as a
first implementation of this technique. In the suggested exercises
appearing at the end of this case study, you will modify this code
slightly to compute averages values of certain observables.
But first, I recommend a visit to the website of Peter Young at UC
Santa Cruz
(http://bartok.ucsc.edu/peter/java/ising/ising.html).
You will see a Java implentation of a Monte Carlo simulation of a
2-dimensional Ising magnet (One of many on the web; google ``ising
simulation'' and you'll get a nice sample.) This is a fun little Java
applet that lets you play with an Ising system. You can change the
temperature of the simulation: making it cold will ``freeze'' the
system, and making it hot ``melts'' it. Near the critical
temperature, ![]() , relatively large regions of mostly-up spins
compete with regions of mostly down spin. In one of the exercises,
we'll learn how to measure an observable called the correlation
length, which characterizes the size of these domains and is a useful
signature of criticality.
, relatively large regions of mostly-up spins
compete with regions of mostly down spin. In one of the exercises,
we'll learn how to measure an observable called the correlation
length, which characterizes the size of these domains and is a useful
signature of criticality.