Thermodynamic integration is a conceptually simple, albeit expensive, way to calculate free energy differences from MC or MD simulations. In this example, we will consider the calculation (again) of chemical potential in a Lennard-Jones fluid at a given temperature and density, a task performed very well already by the Widom method (so long as the densities are not too high.) More details of the method can be found in Reference [15].
We begin with the relation derived in the book for a free energy
difference,
![]() , between two systems which are identical
(same number of particles, density, temperature, etc.) except
that they obey two different potentials. System I obeys
, between two systems which are identical
(same number of particles, density, temperature, etc.) except
that they obey two different potentials. System I obeys
![]() and System II
and System II
![]() . To measure this
free energy difference, we must integrate along a reversible path from
I to II. So let us suppose that we can write a ``metapotential'' that
uses a switching parameter,
. To measure this
free energy difference, we must integrate along a reversible path from
I to II. So let us suppose that we can write a ``metapotential'' that
uses a switching parameter, ![]() , to measure distance along this
path. So, when
, to measure distance along this
path. So, when ![]() , we are in System I, and when
, we are in System I, and when ![]() we
are in System II. One way we might encode this (though this is not
necessarily a general splitting, as we shall see below) is
we
are in System II. One way we might encode this (though this is not
necessarily a general splitting, as we shall see below) is
| (210) |
Let us consider the canonical partition function for a system obeying
a general potential
![]() :
:
| (211) |
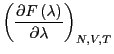 |
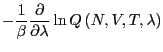 |
(212) | |
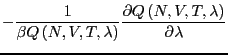 |
(213) | ||
![$\displaystyle \frac{
\begin{minipage}{6cm}
\begin{displaymath}
\int d{\bf r}^N ...
...t[-\beta\mathscr{U}\left(\lambda\right)\right]
\end{displaymath}\end{minipage}}$](img628.png) |
(214) |
The free energy difference between I and II is given by:
| (215) |
To compute ![]() , we imagine two systems: System I has
, we imagine two systems: System I has ![]() ``real'' particles, and 1 ideal gas particle, and system II has
``real'' particles, and 1 ideal gas particle, and system II has ![]() real particles. The two free energies can be written:
real particles. The two free energies can be written:
| (216) | |||
| (217) |
For large values of ![]() , we see that
, we see that
![]() . So, we have another route to compute
. So, we have another route to compute ![]() .
First, we tag a particle
.
First, we tag a particle ![]() , call it the
``
, call it the
``![]() -particle'', and apply the following modified potential to
its pairwise interactions:
-particle'', and apply the following modified potential to
its pairwise interactions:
| (219) |
Next, we conduct many independent MC simulations at various values of
![]() and a given value of
and a given value of ![]() and
and ![]() , generating for each
, generating for each
![]() a table of
a table of
![]() vs.
vs. ![]() which can be integrated to yield a single value for
which can be integrated to yield a single value for
![]() . This turns out to be an expensive way to compute the
chemical potential for a Lennard-Jones fluid, compared to the Widom
method (Sec. 6.1), for at least low to moderate densities.
. This turns out to be an expensive way to compute the
chemical potential for a Lennard-Jones fluid, compared to the Widom
method (Sec. 6.1), for at least low to moderate densities.
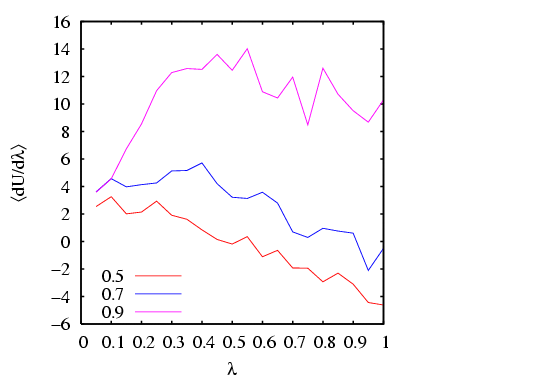
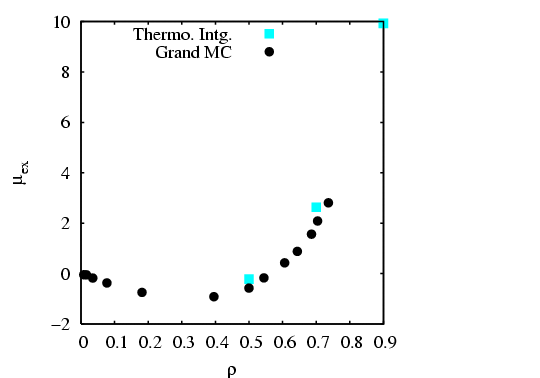
I have done a rough comparison of the thermodynamic integration method
described above to the grand canonical MC simulation technique
described in Sec. 5.1. Below is a plot of
![]() vs.
vs. ![]() for three densities
for three densities
![]() . Each point is computed from a single MC simulation
using the code mclj_ti.c. The
temperature was
. Each point is computed from a single MC simulation
using the code mclj_ti.c. The
temperature was ![]() = 2.0, and run for 10
= 2.0, and run for 10![]() cycles for
cycles for ![]() = 216.
We see that the data is not terribly smooth; it is not clear how
many more cycles would result in smoother data.
= 216.
We see that the data is not terribly smooth; it is not clear how
many more cycles would result in smoother data.
 |
|
|
 |
|
|
Questions: