Ewald Forces

Now, we can use Eq. 334 in a Monte Carlo simulation of a system of charges, provided that periodic boundary conditions are used and the domain is cubic. (Extensions to non-cubic boxes and slab geometries are discussed to a limited extent in F&S.) We can also use the Ewald technique to calculate forces for use in molecular dynamics simulations.

The force on particle $i$ due to the charges in the system is given by

$${\bf F}_i = -\frac{\partial}{\partial{\bf r}_i}\mathscr{U}_{\rm Coul}$$ (337)

For our purposes, the two contributions to ${\bf F}_i$ are due to the $k$-space energy and the short-ranged, real-space energy:

$${\bf F}_i = {\bf F}_i^{(k)} + {\bf F}_i^{(r)}$$ (338)

Notice that there is no change in $\mathscr{U}_{\rm self}$ when ${\bf r}_i$ changes, so no forces arise from $\mathscr{U}_{\rm self}$.

The $k$-space contribution is given by

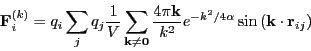$${\bf F}_i^{(k)} = q_i\sum_j q_j \frac{1}{V} \sum_{{\bf k}\ne... ...{k^2}e^{-k^2/4\alpha}\sin\left({\bf k}\cdot{\bf r}_{ij}\right)$$ (339)

The real-space contribution is given by

$${\bf F}_i^{(r)} = q_i\sum_j q_j \left[2\sqrt{\frac{\alpha}{\... ...rfc}(\sqrt{\alpha} r_{ij})\right]\frac{{\bf r}_{ij}}{r_{ij}^2}$$ (340)