

Next: Monte Carlo Simulation
Up: Statistical Mechanics: A Brief
Previous: Entropy and Temperature
Section 2.2 of Frenkel & Smit [1] discusses a
derivation of the ``quasi-classical'' representation of the canonical
partition function,
 :
:
![\begin{displaymath}
Q_{\rm classical} = \frac{1}{h^{dN}N!}\int \int d{\bf r}^N d...
...\left[-\beta\mathscr{H}\left({\bf r}^N,{\bf p}^N\right)\right]
\end{displaymath}](img153.png) |
(42) |
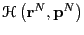 is the Hamiltonian
function which computes the energy of a point in phase space. The
derivation of Eq. 42 is not repeated here. What is
important is that the probability of a point in phase space is
represented as
is the Hamiltonian
function which computes the energy of a point in phase space. The
derivation of Eq. 42 is not repeated here. What is
important is that the probability of a point in phase space is
represented as
![\begin{displaymath}
P\left({\bf r}^N,{\bf p}^N\right) = \left(Q_{\rm classical}\...
...left[-\beta\mathscr{H}\left({\bf r}^N,{\bf p}^N\right)\right].
\end{displaymath}](img155.png) |
(43) |
So, the general ``sum-over-states' ensemble average of quantum
statistical mechanics, first presented in
Eq. 1, becomes an integral over phase space in
classical statistical mechanics:
![\begin{displaymath}
\left<G\right> = \frac{
\mbox{
\begin{minipage}{8cm}
\beg...
...,{\bf p}^N\right)\right]
\end{displaymath} \end{minipage} }},
\end{displaymath}](img156.png) |
(44) |
where
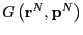 is the value of the
observable
is the value of the
observable 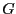 at phase space point
at phase space point
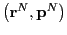 . Before moving on, it is useful to recognize that
we normall simplify this ensemble average by noting that, for a
system of classical particles, the usual choice for the Hamiltonian
has the form
. Before moving on, it is useful to recognize that
we normall simplify this ensemble average by noting that, for a
system of classical particles, the usual choice for the Hamiltonian
has the form
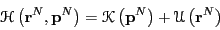 |
(45) |
where 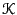 is the kinetic energy, which is only a function of
momenta, and
is the kinetic energy, which is only a function of
momenta, and 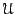 is the potential energy, which is only a
function of position. The canonical partition function,
is the potential energy, which is only a
function of position. The canonical partition function, 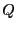 , can in
this case be factorized:
, can in
this case be factorized:
The quantity in the left-hand braces is the ideal gas partition
function, because it corresponds to the case when the potential
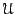 is 0. (Note that we have multiplied and divided by
is 0. (Note that we have multiplied and divided by
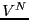 ; this is the equivalent of scaling the positions in the
integration over positions.) The quantity in the right-hand braces
is called the configurational partition function,
; this is the equivalent of scaling the positions in the
integration over positions.) The quantity in the right-hand braces
is called the configurational partition function, 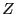 .
.
Because the kinetic energy 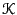 has the simple form,
has the simple form,
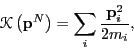 |
(49) |
where 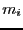 is the mass of particle
is the mass of particle 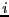 , the integral over particle
momenta can be evaluated analytically:
, the integral over particle
momenta can be evaluated analytically:
(We have assumed all particles have the same mass, 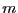 ; in the case
of distinct masses, this is just a product of similar factors.)
; in the case
of distinct masses, this is just a product of similar factors.)
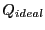 becomes
becomes
where 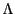 is the de Broglie wavelength.
is the de Broglie wavelength.
So, when the observable 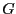 is a function of positions only, the
ensemble average becomes a configurational average:
is a function of positions only, the
ensemble average becomes a configurational average:
![\begin{displaymath}
\left<G\right> = Z^{-1}\int d{\bf r}^N \exp\left[-\beta\mathscr{U}\left({\bf r}^N\right)\right] G\left({\bf r}^N\right).
\end{displaymath}](img179.png) |
(54) |
Note that the integation over momentum yields a factor 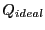 in
both the numerator and denominator, and thus divides out. We can write
this configurational average using a probability distribution,
in
both the numerator and denominator, and thus divides out. We can write
this configurational average using a probability distribution, 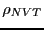 ,
as
,
as
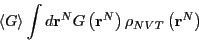 |
(55) |
where
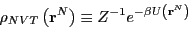 |
(56) |
is called the ``canonical probability distribution.'' As pointed out
on p. 15 of Frenkel & Smit [1],
Eq. 54 is ``the starting point for virtually all
classical simulations of many-body systems''; that is, it is the
starting point for all simulations discussed in this course.


Next: Monte Carlo Simulation
Up: Statistical Mechanics: A Brief
Previous: Entropy and Temperature
cfa22@drexel.edu
![]() :
:
![]() has the simple form,
has the simple form,
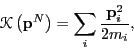
![$\displaystyle \int d{\bf p}^N \exp\left[-\beta\mathscr{K}\left({\bf p}^N\right)\right]$](img170.png)
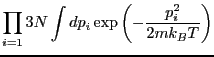
![]() becomes
becomes
![$\displaystyle \frac{V^N}{N!h^{3N}} \int d{\bf p}^N \exp\left[-\beta\mathscr{K}\left({\bf p}^N\right)\right]$](img174.png)
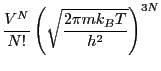

![]() is a function of positions only, the
ensemble average becomes a configurational average:
is a function of positions only, the
ensemble average becomes a configurational average: