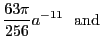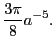

Next: Bibliography
Up: Odds and Ends
Previous: Odds and Ends
Lennard-Jones on a Line
Imagine a particle (the ``probe'') fixed at a distance 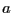 from a line
of populated by particles . The
probe and particles on the line interact via a pairwise potential:
from a line
of populated by particles . The
probe and particles on the line interact via a pairwise potential:
![\begin{displaymath}
u(r) = 4\left[r^{-12}-r^{-6}\right]
\end{displaymath}](img1024.png) |
(360) |
This is the Lennard-Jones potential in reduced units. The particles
on the line do not interact with each other, but they remain fixed on
the line.
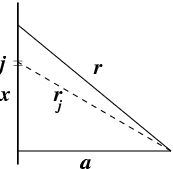 |
Notation. A probe particle lies at a distance 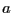 from
a line (the from
a line (the 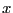 -axis) populated by Lennard-Jones particles. The line
is divided into ``cells'' indexed by -axis) populated by Lennard-Jones particles. The line
is divided into ``cells'' indexed by 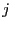 , and the interaction of the
probe with a particle in cell , and the interaction of the
probe with a particle in cell 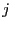 depends on the distance depends on the distance 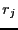 . . |
Let us now write the total potential. We do not know exactly where
the fixed particles are on the line, so we do the following. Divide
the 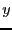 -axis into an infinite number of finitely-sized divisions, or
``cells,'' indexed by a counter
-axis into an infinite number of finitely-sized divisions, or
``cells,'' indexed by a counter 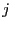 . Let the quantity
. Let the quantity 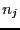 be the
occupation number of division
be the
occupation number of division 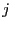 , which is 0 if the division is
unoccupied, and 1 if it is occupied. We must make the assumption that
the cells are so small that there can either be one or no particles in
any cell. We can write the total potential by summing over all
cells:
, which is 0 if the division is
unoccupied, and 1 if it is occupied. We must make the assumption that
the cells are so small that there can either be one or no particles in
any cell. We can write the total potential by summing over all
cells:
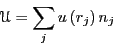 |
(361) |
where 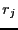 is the distance from the probe to cell
is the distance from the probe to cell 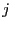 . Now we
can pass into the continuum limit by considering that
. Now we
can pass into the continuum limit by considering that
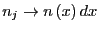 , where
, where
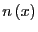 is the density of
particles on the line, and thus
is the density of
particles on the line, and thus 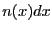 is the number of particles on
the line between
is the number of particles on
the line between 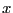 and
and 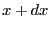 . So, in a continuum representation:
. So, in a continuum representation:
where we have used the Pythagorean theorem:
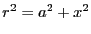 . We
seek a representation
. We
seek a representation
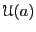 , that is, the potential of the
system as a function of the distance of the probe to the line.
, that is, the potential of the
system as a function of the distance of the probe to the line.
Now, let us assume that the density of particles on the line is
uniform and equal to 1 particle per unit length:
We can express Eq. 363 as
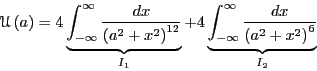 |
(364) |
At this point we turn to integral tables. Dwight [28]
reports on p. 213 in integral # 856.21
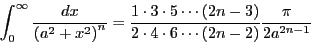 |
(365) |
Both integrals 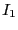 and
and 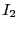 in Eq. 365 are even.
Applying Eq. 366, we find
in Eq. 365 are even.
Applying Eq. 366, we find
This leaves us with
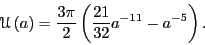 |
(368) |
Note that the potential now displays an ``11-5'' distance dependence.
The figure below shows
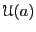 together with the raw
Lennard-Jones 12-6 potential (Eq. 361).
together with the raw
Lennard-Jones 12-6 potential (Eq. 361).
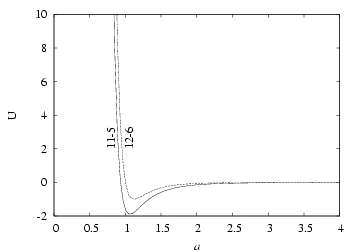 |
The 11-5 potential
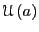 as a function
of distance to the line, as a function
of distance to the line, 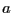 , together with the 12-6 Lennard-Jones
potential used to derive it. , together with the 12-6 Lennard-Jones
potential used to derive it. |


Next: Bibliography
Up: Odds and Ends
Previous: Odds and Ends
cfa22@drexel.edu
![]() from a line
of populated by particles . The
probe and particles on the line interact via a pairwise potential:
from a line
of populated by particles . The
probe and particles on the line interact via a pairwise potential:

![]() and
and ![]() in Eq. 365 are even.
Applying Eq. 366, we find
in Eq. 365 are even.
Applying Eq. 366, we find