A C Code for the 2D Ising Magnet

In this section, we will dissect piece-by-piece a small C program that implements an NVT Metropolis Monte Carlo simulation of a 2D Ising magnet.

If you have not already done so, clone the Abrams-Teaching/instructional-codes repository from Github. This repository will be updated throughout the term with source code in the originals subdirectory. You should create a subdirectory called my_work inside this repository and do all editing, compiling, and running in there. This directory is specifically excluded from git revision control by its inclusion in the .gitignore file. This way, when I put new codes in the repository, you only have to git pull to download them.

cd
cd cheT580
git clone git@github.com:Abrams-Teaching/instructional-codes.git
cd instructional-codes
mkdir my_work
cd my_work
cp ../originals/ising_mc.c .
code .

From a terminal command-line inside VSCode, or outside, you can compile ising_mc.c via

gcc -O3 -o ising ising_mc.c -lm -lgsl

and you can then run it at the command line as ./ising. It has a lot of options for controlling the size of the magnet (the number of spins), the temperature, and other parameters, which I'll go over now.

ising_mc.c conducts a canoncial Metropolis Monte Carlo simulation of an Ising magnet of size $L\times L$ at temperature $T$ (both specified by the user at run time on the command line), and it computes both the average energy per spin $\left<\epsilon\right>$ and the average spin value, $\left<s_1\right>$.

Periodic boundaries are employed in calculating the nearest-neighbor interactions. Consider an $L\times L$ magnet; each row $i$ indexed from 0 to $N-1$ has $L$ columns also indexed from 0 to $N-1$. If the cell at (5,5) queries its neighbors, they are at (4,5), (6,5), (5,4), and (5,6). However, the cell at (0,5) would have a southern neighbor at ($N-1$,5) instead of (-1,5), since there is no row indexed -1! Fig. 3 demonstrates this.

Figure 3: Schematic Ising magnet highlighting periodic boundary conditions. The neighbors of the red spin can be found by adding or subtracting one from the cell's row and column index. For the green and blue cells, however, at least one of the neighbors appears on the other side of the magnet.

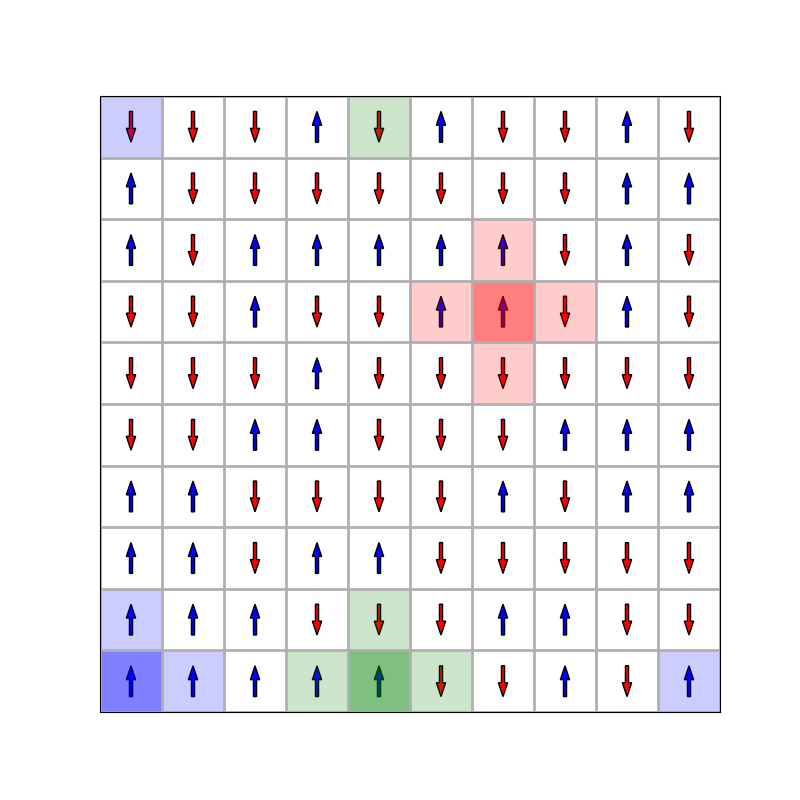An abbreviated listing of the code follows. Some comments in the full, downloadable code have been omitted for space, and I have instead explained each code fragment in accompanying text.