Next: Histogram Reweighting Up: Free Energy Methods Previous: Thermodynamic Integration
One interesting feature of the Widom method is that the only trial move is insertion; however, the free-energy difference between an ![]() -particle system and an
-particle system and an ![]() -particle system should not depend on which direction the trial moves take. If we imagine a “Widom real-particle removal” method, we'd write the chemical potential as
-particle system should not depend on which direction the trial moves take. If we imagine a “Widom real-particle removal” method, we'd write the chemical potential as
| (327) |
Sampling
![]() in a straightforward NVT MC simulation won't work, however, because...
in a straightforward NVT MC simulation won't work, however, because...
There is, however, a right way to use bidirectional energy changes to compute free-energy differences, termed the “overlapping distribution method” and attributed to Bennett [44].
Consider two systems 0 and 1, obeying potentials
![]() and
and
![]() , respectively. Let
, respectively. Let ![]() be the scaled configurational integral of the Boltzmann factor:
be the scaled configurational integral of the Boltzmann factor:
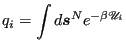 |
(328) |
We can then express the free energy difference between these systems as (assuming for simplicity they have the same volumes):
| (329) |
Consider next we run an NVT MC simulation on
![]() and sample
and sample
![]() . Formally, the probability density of
. Formally, the probability density of
![]() from this simulation is
from this simulation is
| (334) | ||
| (335) |
Bennett[44] suggests the following transformation of ![]() and
and ![]() to permit easy calculation of
to permit easy calculation of ![]() . Letting
. Letting
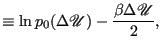 and and |
(336) | |
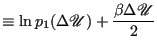 |
(337) |
| (338) |
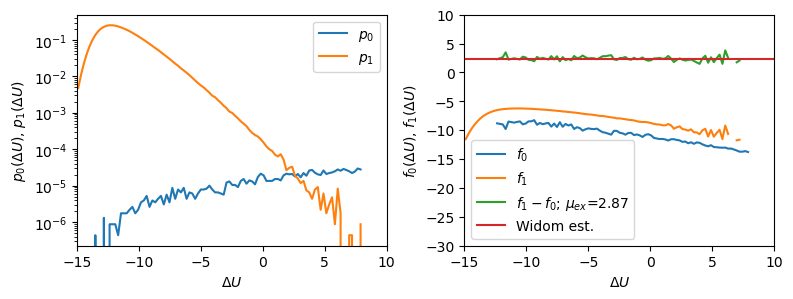
Suppose we now take the example of system 1 with ![]() real particles and system 0 with
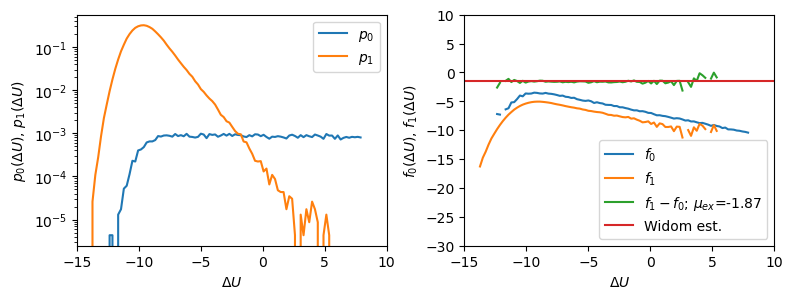
real particles and system 0 with ![]() real particles and one ideal-gas particle. The free-energy change from 0 to 1 is the excess chemical potential (yet again!). Fig. 41 illustrates using Bennett's method to compute
real particles and one ideal-gas particle. The free-energy change from 0 to 1 is the excess chemical potential (yet again!). Fig. 41 illustrates using Bennett's method to compute
![]() of the Lennard-Jones fluid at
of the Lennard-Jones fluid at ![]() = 1.2 for a few different densities. For each density, two simulations were run: simulation-0 computes the distribution of
= 1.2 for a few different densities. For each density, two simulations were run: simulation-0 computes the distribution of
![]() , the energy associated with converting the ideal-gas particle to a real particle, while simulation-1 computes the same distribution for converting a randomly chosen particle from being an ideal-gas particle to being a real particle. This latter
, the energy associated with converting the ideal-gas particle to a real particle, while simulation-1 computes the same distribution for converting a randomly chosen particle from being an ideal-gas particle to being a real particle. This latter
![]() is easily computed using the single-particle energy function
is easily computed using the single-particle energy function e_i. It is important to note that the direction of the ![]() is from ideal-gas to real for both simulations. Note too that since we sample
is from ideal-gas to real for both simulations. Note too that since we sample
![]() for particle insertion in simulation-0, we can just as easily compute the expectation
for particle insertion in simulation-0, we can just as easily compute the expectation
![]() and thereby get a direct estimate of
and thereby get a direct estimate of
![]() .
.
At the moderately low density of ![]() = 0.7, we see a clear constant offset
= 0.7, we see a clear constant offset
![]() between
between ![]() and
and ![]() . Note clear agreement between the offset over a finite-size domain of
. Note clear agreement between the offset over a finite-size domain of
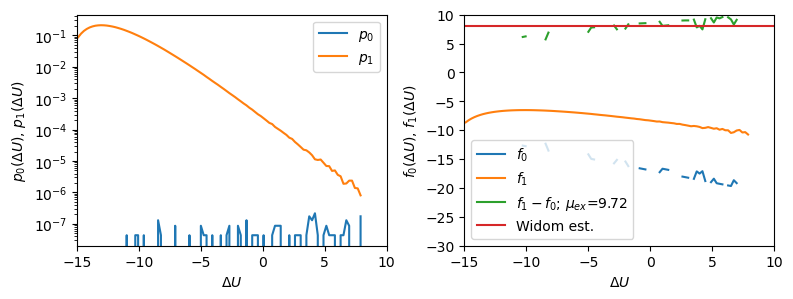
![]() and the single-point Widom estimate. For the somewhat higher density of 0.9, the offset is a bit noisier, reflecting somewhat poorer sampling. For the highest density, the sampling in simulation-0 is so poor that it is nearly impossible to detect an overlap domain.
and the single-point Widom estimate. For the somewhat higher density of 0.9, the offset is a bit noisier, reflecting somewhat poorer sampling. For the highest density, the sampling in simulation-0 is so poor that it is nearly impossible to detect an overlap domain.
 |
cfa22@drexel.edu