Well-Tempered Metadynamics

In the well-tempered variant [49] of metadynamics, The weight 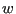$w$ is augmented with a Boltzmann factor that diminishes exponentially as 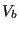$V_b$ builds up:

$$V_b(\theta,t) = w\sum_{t^\prime < t}\exp\left[-\frac{V_b(\theta(t... ...] \exp\left(-\frac{\left[\theta(t^\prime)-\theta(t)\right]^2}{2\sigma^2}\right)$$ (365)

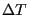$\Delta T$ is the so-called “bias temperature”, and it acts to diminish the contribution to 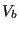$V_b$ at any 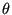$\theta$ as time progresses, leading to a converged bias potential. The free energy is reconstructed by an inversion of the converged bias potential that requires the bias temperature:

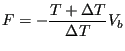$$F = -\frac{T+\Delta T}{\Delta T}V_b$$ (366)

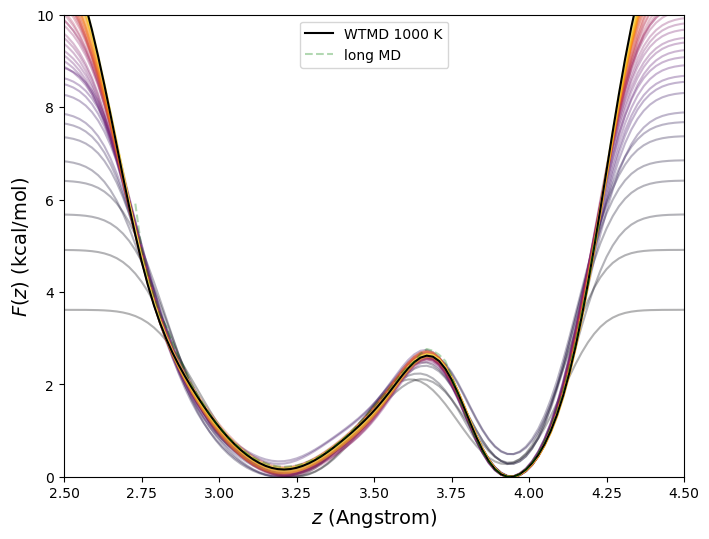
Fig. 48 shows the free energy vs. C1-C4 distance for butane at 273 K computed using well-tempered metadynamics with parameters identical to the standard metadynamics run of the previous section but with a bias temperature of 1000 K.

Figure 48: Free energy in kcal/mol vs. C1-C4 distance in Å, for butane in vacuum at 273 K computed using MD (green dash) and well-tempered metadynamics (black solid). The MD simulation was run for 10$^8$ timesteps, and the metadynamics for 10$^7$. The bias temperature for well-biased metadynamics was 1000 K. Intermediate values of the metadynamics free energy are also shown color-coded from purple (early) to yellow (late). The final metadynamics free energy is the average over all free-energy snapshots (i.e., it is the time-average negative bias potential).