Analytical Potentials

The total system potential energy is most often computed by means of analytical potentials. Such a potential energy can be written as a continuous function of the positions of particle centers-of-mass. (Such potentials are often termed ``empirical'' when applied to atomic systems because they formally neglect quantum mechanics.) In most molecular simulations, the total system potential can be decomposed in the following way:

$$\mathscr{U}\left({\bf r}^N\right) = U_0 + \sum_i U_1( {\bf r... ... ) + \cdots + U_N( {\bf r}_i, {\bf r}_j, \dots , {\bf r}_N ),$$ (80)

Here, $U_0$ is some reference potential. $U_1$ is a ``one-body'' potential, $U_2$ is a ``two-body'' potential, etc. This generally defines a ``many-body'' potential, and is the heart of the ``many-body'' problem of statistical physics. Namely, the Boltzmann factor $e^{-\beta\mathscr{U}}$ correlates every position with every other position, and the configurational integral (Eq. 54) is not factorizable into many separate easily evaluated integrals.

Analytical potentials are most easily understood by considering model systems which are decomposable into spherically-symmetric, pairwise interactions. Consider then the following total system potential energy:

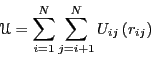$$\mathscr{U} = \sum_{i=1}^{N}\sum_{j=i+1}^{N} U_{ij}\left(r_{ij}\right)$$ (81)

The double-sum runs over all unique pairs of particles. The function $U_{ij}\left(r_{ij}\right)$ is called a pair potential, and it is a function of the scalar distance between particle $i$ and $j$.

The simplest pair potential is the ``hard-sphere'':

$$U_{HS}\left(r\right) = \left\{\begin{array}{ll} \infty & r < \sigma\\ 0 & r > \sigma \end{array}\right.$$ (82)

Here, $\sigma$ is an arbitrary interaction range that denotes the ``size'' of the spheres. When the distance between two spheres is less than $\sigma$, the energy is infinite; otherwise it is 0. This is the simplest way to enforce excluded volume among spherical particles in an MC simulation. We will see an implementation of a hard-sphere liquid in the next section.

The most celebrated pair potential is the Lennard-Jones potential:

$$U_{LJ}\left(r\right) = 4\epsilon\left[\left(\frac{\sigma}{r}\right)^{12}-\left(\frac{\sigma}{r}\right)^{6}\right]$$ (83)

$\epsilon$ is the unit of energy, and is the well-depth of the pair potential (that is, it is the minimum value of the potential). $\sigma$ is the unit of length, and is the separation distance when the potential is identically zero. Unlike the hard-sphere potential (Eq. 82), the Lennard-Jones potential is ``smooth'' (it has a continuous first derivative). This smoothness makes it useful in Molecular Dynamics simulations, as we will see later in the course.

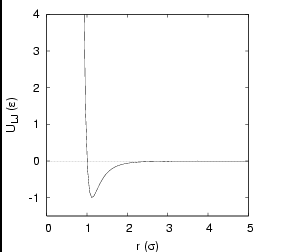The Lennard-Jones pair potential.

We will encounter more complex potentials than Lennard-Jones, but it serves as a useful tool for introductory molecular simulation.

Reduced Units. Because the Lennard-Jones potential is so prevalent in molecular simulation, it is essential that we understand the unit system most often chosen for simulations using this potential. For computational simplicity, energy in a Lennard-Jones system is measured in units of $\epsilon$ and length in $\sigma$. This means that everywhere in the code you would expect to see $\epsilon$ or $\sigma$, you find a 1.

Now, to compute the total potential $\mathscr{U}$ for a system of particles, the simplest algorithm is to loop over all unique pairs of particles. Here is a simple pair search C function (the so-called $N^2$ algorithm because its complexity scales like $N^2$) to compute the total energy of a system of Lennard-Jones particles, in reduced units:

double total_e ( double * rx, double * ry, double * rz, int n ) {
   int i,j;
   double dx, dy, dz, r2, r6, r12;
   double e = 0.0;

   for (i=0;i<(n-1);i++) {
     for (j=i+1;j<n;j++) {
        dx  = (rx[i]-rx[j]);
        dy  = (ry[i]-ry[j]);
        dz  = (rz[i]-rz[j]);
        r2  = dx*dx + dy*dy + dz*dz;
        r6  = r2*r2*r2;
        r12 = r6*r6;
        e  += 4*(1.0/r12 - 1.0/r6); 
     }
   }
   return e;
}

Although it is strictly correct, the $N^2$ pair search algorithm is inefficient if there is a finite interaction range in the pair potential. Typically in dense liquid simulations, a Lennard-Jones pair potential is truncated at $r = 2.5 \sigma$. There are some potentials that are cut off at even shorter distances. The point is that, when the maximum interaction distance is finite, each particle has a finite maximum number of interaction partners. (This assumes number density is bounded, which is a reasonable assumption.) More advanced techniques (which we discuss later) can be invoked to make the pair search much more efficient in this case. The two most common are (1) the Verlet list, and (2) the link-cell list. For now, and to keep the presentation simple, we will stick to the inefficient, brute-force $N^2$ algorithm.