

Next: Case Study 1: The
Up: Monte Carlo Simulation
Previous: Monte Carlo Simulation
The Metropolis Monte Carlo Method
Monte Carlo is in general a technique for performing numerical
integration. Consider the following integral:
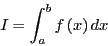 |
(57) |
Now imagine that we have a second function, 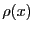 , which is positive
in the interval
, which is positive
in the interval ![$[a,b]$](img185.png) . We can also express
. We can also express 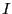 as
as
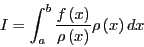 |
(58) |
If we think of
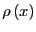 as a probability density,
then what we have just expressed is the average of the quantity
as a probability density,
then what we have just expressed is the average of the quantity
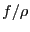 on
on 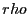 in the interval
in the interval ![$[a,b]$](img185.png) :
:
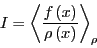 |
(59) |
This implies that we can approximate 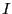 by picking
by picking 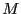 values
values
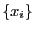 randomly out of the probability distribution
randomly out of the probability distribution 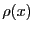 and computing
the following sum:
and computing
the following sum:
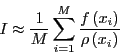 |
(60) |
Note that this approximates the mean of 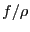 as long as pick a
large enough number of random numbers (
as long as pick a
large enough number of random numbers (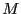 is large enough) such that
we ``densely'' cover the interval
is large enough) such that
we ``densely'' cover the interval ![$[a,b]$](img185.png) . If
. If
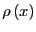 is
uniform on
is
uniform on ![$[a,b]$](img185.png) ,
,
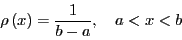 |
(61) |
and therefore,
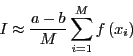 |
(62) |
The next question is, how good an approximation is this, compared with
more traditional one-dimensional numerical integration techniques,
such as Simpson's rule and quadrature? A better phrasing of this
question is, how expensive is this technique for a given level of
accuracy, compared to traditional techniques? Consider this means to
compute  :
:
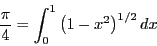 |
(63) |
Allen and Tildesley [2] mention that, in order
use Eq. 62 to compute 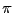 to an accuracy of one part
in 10
to an accuracy of one part
in 10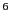 requires
requires 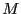 = 10
= 10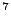 random values of
random values of 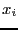 , whereas
Simpson's rule required three orders of magnitude fewer points
to discretize the interval to obtain an accuracy of one part in
10
, whereas
Simpson's rule required three orders of magnitude fewer points
to discretize the interval to obtain an accuracy of one part in
10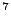 . So the answer is, integral estimation using uniform random
variates is expensive.
. So the answer is, integral estimation using uniform random
variates is expensive.
But, the situation changes radically when the dimensionality of the
integral is large, as is the case for an ensemble average. For
example, for 100 particles having 300 coordinates, the configurational
average
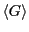 (Eq. 54) could be
discretized using Simpson's rule. If we did that, requesting only a
modest 10 points per axis in configurational space, we would need to
evaluate the integrand
(Eq. 54) could be
discretized using Simpson's rule. If we did that, requesting only a
modest 10 points per axis in configurational space, we would need to
evaluate the integrand
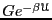
10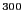
times. This is an almost unimaginably large number (a googul cubed).
Using a direct numerical technique to compute statistical mechanical
averages is simply out of the question.
We therefore return to the idea of evaluating the integrand at a
discrete set of points selected randomly from a distribution. Here we
call upon the idea of importance sampling. Let us try to use
whatever we know ahead of time about the integrand in picking our
random distribution, 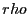 , such that we minimize the number of
points (i.e., the expense) necessary to give an estimate of
, such that we minimize the number of
points (i.e., the expense) necessary to give an estimate of
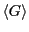 to a given level of accuracy.
to a given level of accuracy.
Now, clearly the states that contribute the most to the integrals we
wish to evaluate by configurational averaging are those states with
large Boltzmann factors; that is, those states for which 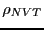 is large. It stands to reason that if we randomly select points from
is large. It stands to reason that if we randomly select points from
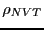 , we will do a pretty good job approximating the integral.
So what we end up computing is the ``average of
, we will do a pretty good job approximating the integral.
So what we end up computing is the ``average of 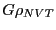 over
over
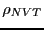 '':
'':
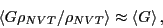 |
(64) |
which should give an excellent approximation for
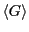 .
The idea of using the
.
The idea of using the 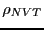 as the sampling distribution is due
to Metropolis et al. [6]. This makes the real work
in computing
as the sampling distribution is due
to Metropolis et al. [6]. This makes the real work
in computing
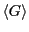 generating states that randomly sample
generating states that randomly sample
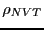 .
.
Metropolis et al. [6] showed that an efficient way to
do this involves generating a Markov chain of states which is
constructed such that its limiting distribution is 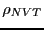 . A
Markov chain is just a sequence of trials, where (i) each trial
outcome is a member of a finite set called ``state space,'' and (ii)
every trial outcome depends only on the outcome that immediately
precedes it. By ``limiting distribution,'' we mean that the trial
acceptance probabilities are tuned such that the probability of
observing the Markov chain atop a particular state is defined by some
equilibrium probability distribution,
. A
Markov chain is just a sequence of trials, where (i) each trial
outcome is a member of a finite set called ``state space,'' and (ii)
every trial outcome depends only on the outcome that immediately
precedes it. By ``limiting distribution,'' we mean that the trial
acceptance probabilities are tuned such that the probability of
observing the Markov chain atop a particular state is defined by some
equilibrium probability distribution, 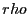 . For the following
discussion, it will be convenient to denote a particular state
. For the following
discussion, it will be convenient to denote a particular state 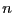 using
using 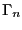 , instead of
, instead of 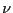 .
.
A trial is some perturbation (usually small) of the coordinates
specifying a state. For example, in an Ising system, this might mean
flipping a randomly selected spin. In a system of particles in
continuous space, it might mean displacing a randomly selected
particle by a small amount 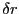 in a randomly chosen direction.
There is a large variety of such ``trial moves'' for any particular
system; we will only deal with a few simple ones in this course.
in a randomly chosen direction.
There is a large variety of such ``trial moves'' for any particular
system; we will only deal with a few simple ones in this course.
The probability that a trial move results in a successful transition
from state 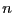 to
to 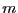 is denoted
is denoted 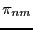 and
and 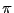 is called
the ``transition matrix.'' It must be specified ahead of time to
execute a traditional Markov chain. Since the probability that a
trial results in a successful transition to any state, the rows
of
is called
the ``transition matrix.'' It must be specified ahead of time to
execute a traditional Markov chain. Since the probability that a
trial results in a successful transition to any state, the rows
of 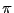 add to unity:
add to unity:
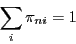 |
(65) |
With this specification, we term 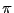 a ``stochastic'' matrix.
Furthermore, for an equilibrium ensemble of states in state space, we
require that transitions from state to state do not alter state
weights as determined by the limiting distribution. So the weight of
state
a ``stochastic'' matrix.
Furthermore, for an equilibrium ensemble of states in state space, we
require that transitions from state to state do not alter state
weights as determined by the limiting distribution. So the weight of
state 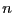 :
:
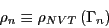 |
(66) |
must be the result of transitions from all other states to state 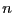 :
:
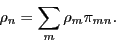 |
(67) |
For all states 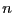 , we can write Eq. 67 as a post-op matrix
equation:
, we can write Eq. 67 as a post-op matrix
equation:
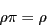 |
(68) |
where 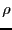 is the row vector of all state weights.
Eq. 68 constrains our choice of
is the row vector of all state weights.
Eq. 68 constrains our choice of 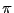 . This means
there is still more than one way to specify
. This means
there is still more than one way to specify 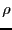 . Metropolis
et al. [6] suggested:
. Metropolis
et al. [6] suggested:
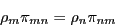 |
(69) |
That is, the probability of transitioning from state 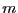 to
to 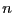 is
exactly equal to the probability of transitioning from state
is
exactly equal to the probability of transitioning from state 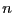 to
to
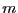 . This is called the ``detailed balance'' condition, and it
guarantees that the state weights remain static. Observe:
. This is called the ``detailed balance'' condition, and it
guarantees that the state weights remain static. Observe:
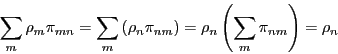 |
(70) |
Detailed balance is, however, overly restrictive; this fact is of
little importance in this course.
Metropolis et al. [6] chose to construct 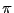 as
as
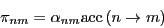 |
(71) |
where 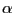 is the probability that a trial move is attempted, and
is the probability that a trial move is attempted, and
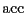 is the probability that a move is accepted. If the
probability of proposing a move from
is the probability that a move is accepted. If the
probability of proposing a move from 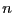 to
to 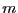 is equal to that
of proposing a move from
is equal to that
of proposing a move from 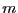 to
to 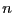 , then
, then
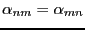 , and the detailed balance condition is written:
, and the detailed balance condition is written:
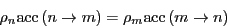 |
(72) |
from which follows
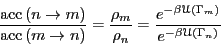 |
(73) |
giving
![\begin{displaymath}
\frac{{\rm acc}\left(n\rightarrow m\right)}{{\rm acc}\left(m...
...]\right\} \equiv \exp\left(-\beta\Delta\mathscr{U}_{nm}\right)
\end{displaymath}](img220.png) |
(74) |
where we have defined the change in potential energy as
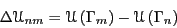 |
(75) |
There are many choices for
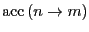 that satisfy Eq. 74. The original choice of Metropolis is
used most frequently:
that satisfy Eq. 74. The original choice of Metropolis is
used most frequently:
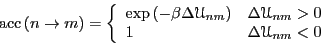 |
(76) |
So, suppose we have some initial configuration 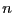 with potential
energy
with potential
energy 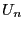 . We make a trial move, temporarily generating a
new configuration
. We make a trial move, temporarily generating a
new configuration 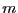 . Now we calculate a new energy,
. Now we calculate a new energy, 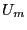 . If this
energy is lower than the original, (
. If this
energy is lower than the original, (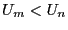 ) we unconditionally
accept the move, and configuration
) we unconditionally
accept the move, and configuration 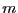 becomes the current
configuration. If it is greater than the original, (
becomes the current
configuration. If it is greater than the original, (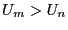 ) we
accept it with a probability consistent with the fact that the states
both belong to a canonical ensemble. How does one in practice decide
whether to accept the move? One first picks a uniform random variate
) we
accept it with a probability consistent with the fact that the states
both belong to a canonical ensemble. How does one in practice decide
whether to accept the move? One first picks a uniform random variate
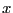 on the interval
on the interval ![$[0,1]$](img228.png) . If
. If
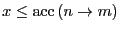 , the move is accepted.
, the move is accepted.
The next section is devoted to an implementation of the Metropolis
Monte Carlo method for a 2D Ising magnet.


Next: Case Study 1: The
Up: Monte Carlo Simulation
Previous: Monte Carlo Simulation
cfa22@drexel.edu
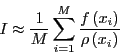
![]() :
:
![]() (Eq. 54) could be
discretized using Simpson's rule. If we did that, requesting only a
modest 10 points per axis in configurational space, we would need to
evaluate the integrand
(Eq. 54) could be
discretized using Simpson's rule. If we did that, requesting only a
modest 10 points per axis in configurational space, we would need to
evaluate the integrand
![]()
![]() , such that we minimize the number of
points (i.e., the expense) necessary to give an estimate of
, such that we minimize the number of
points (i.e., the expense) necessary to give an estimate of
![]() to a given level of accuracy.
to a given level of accuracy.
![]() is large. It stands to reason that if we randomly select points from
is large. It stands to reason that if we randomly select points from
![]() , we will do a pretty good job approximating the integral.
So what we end up computing is the ``average of
, we will do a pretty good job approximating the integral.
So what we end up computing is the ``average of ![]() over
over
![]() '':
'':
![]() . A
Markov chain is just a sequence of trials, where (i) each trial
outcome is a member of a finite set called ``state space,'' and (ii)
every trial outcome depends only on the outcome that immediately
precedes it. By ``limiting distribution,'' we mean that the trial
acceptance probabilities are tuned such that the probability of
observing the Markov chain atop a particular state is defined by some
equilibrium probability distribution,
. A
Markov chain is just a sequence of trials, where (i) each trial
outcome is a member of a finite set called ``state space,'' and (ii)
every trial outcome depends only on the outcome that immediately
precedes it. By ``limiting distribution,'' we mean that the trial
acceptance probabilities are tuned such that the probability of
observing the Markov chain atop a particular state is defined by some
equilibrium probability distribution, ![]() . For the following
discussion, it will be convenient to denote a particular state
. For the following
discussion, it will be convenient to denote a particular state ![]() using
using ![]() , instead of
, instead of ![]() .
.
![]() in a randomly chosen direction.
There is a large variety of such ``trial moves'' for any particular
system; we will only deal with a few simple ones in this course.
in a randomly chosen direction.
There is a large variety of such ``trial moves'' for any particular
system; we will only deal with a few simple ones in this course.
![]() to
to ![]() is denoted
is denoted ![]() and
and ![]() is called
the ``transition matrix.'' It must be specified ahead of time to
execute a traditional Markov chain. Since the probability that a
trial results in a successful transition to any state, the rows
of
is called
the ``transition matrix.'' It must be specified ahead of time to
execute a traditional Markov chain. Since the probability that a
trial results in a successful transition to any state, the rows
of ![]() add to unity:
add to unity:
![]() , we can write Eq. 67 as a post-op matrix
equation:
, we can write Eq. 67 as a post-op matrix
equation:
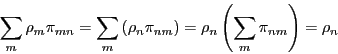
![]() as
as
![]() that satisfy Eq. 74. The original choice of Metropolis is
used most frequently:
that satisfy Eq. 74. The original choice of Metropolis is
used most frequently: