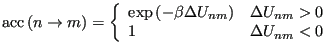The Metropolis Monte Carlo Method
Monte Carlo is a type of numerical integration. Consider the following integral:
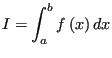 |
(62) |
Now imagine that we have a second function, 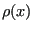 , which is positive in the interval
, which is positive in the interval ![$ [a,b]$](img214.png) . We can also express
. We can also express 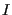 as
as
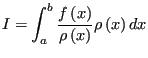 |
(63) |
If we think of
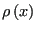 as a probability density, then what we have just expressed is the expectation value of the quantity
as a probability density, then what we have just expressed is the expectation value of the quantity 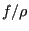 on
on 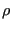 in the interval
in the interval ![$ [a,b]$](img214.png) :
:
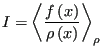 |
(64) |
This implies that we can approximate 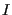 by picking
by picking 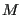 values
values
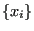 randomly out of the probability distribution
randomly out of the probability distribution 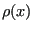 and computing the following sum:
and computing the following sum:
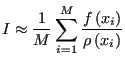 |
(65) |
Note that this approximates the mean of 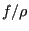 as long as we pick a large enough number of random numbers (
as long as we pick a large enough number of random numbers (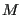 is large enough) such that we “densely” cover the interval
is large enough) such that we “densely” cover the interval ![$ [a,b]$](img214.png) . If
. If
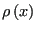 is uniform on
is uniform on ![$ [a,b]$](img214.png) ,
,
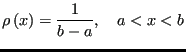 |
(66) |
and therefore,
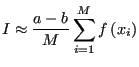 |
(67) |
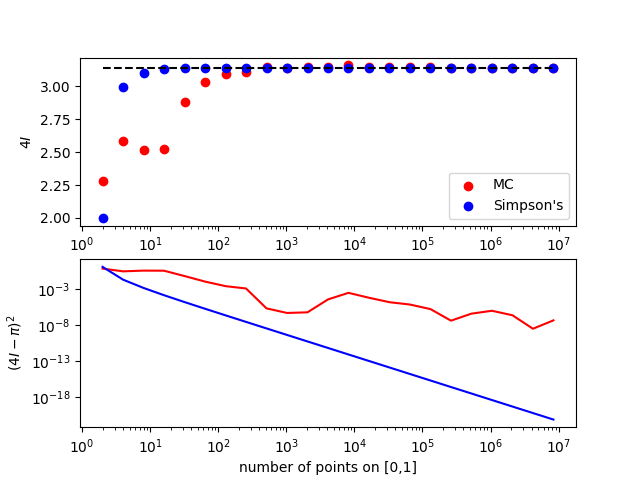
The next question is, how good an approximation is this, compared with other one-dimensional numerical integration techniques, such as Simpson's rule and quadrature? A better phrasing of this question is, how expensive is this technique for a given level of accuracy, compared to traditional techniques? Consider this means to compute 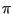 :
:
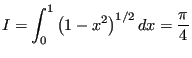 |
(68) |
Allen and Tildesley [2] mention that, in order use Eq. 67 to compute 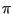 to an accuracy of one part in 10
to an accuracy of one part in 10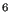 requires
requires 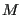 = 10
= 10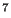 random values of
random values of 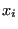 , whereas Simpson's rule requires three orders of magnitude fewer points to discretize the interval to obtain an accuracy of one part in 10
, whereas Simpson's rule requires three orders of magnitude fewer points to discretize the interval to obtain an accuracy of one part in 10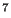 (Fig. 2). So the answer is, integral estimation using Monte Carlo estimation with uniform random variates is expensive.
(Fig. 2). So the answer is, integral estimation using Monte Carlo estimation with uniform random variates is expensive.
But, the situation changes radically when the dimensionality of the integral is large, as is the case for an ensemble average. For example, for a system of 100 particles comprising 300 coordinates, the configurational average
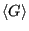 (Eq. 59) could be discretized using Simpson's rule. If we did that, requesting only a modest 10 discrete points per axis in configurational space, we would need to evaluate the integrand
(Eq. 59) could be discretized using Simpson's rule. If we did that, requesting only a modest 10 discrete points per axis in configurational space, we would need to evaluate the integrand
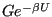 10
10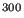 times. This is an almost unimaginably large number. Using a direct numerical technique to compute statistical mechanical averages is simply out of the question.
times. This is an almost unimaginably large number. Using a direct numerical technique to compute statistical mechanical averages is simply out of the question.
We therefore return to the idea of evaluating the integrand at a discrete set of points selected randomly from a distribution. Here we call upon the idea of importance sampling. Let us try to use whatever we know ahead of time about the integrand in picking our random distribution,  , such that we minimize the number of points (i.e., the expense) necessary to give an estimate of
, such that we minimize the number of points (i.e., the expense) necessary to give an estimate of
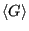 to a given level of accuracy.
to a given level of accuracy.
Now, clearly the states that contribute the most to the integrals we wish to evaluate by configurational averaging are those states with large Boltzmann factors; that is, those states for which
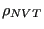 is large. It stands to reason that if we randomly select points from
is large. It stands to reason that if we randomly select points from
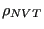 , we will do a pretty good job approximating the integral. So what we end up computing is the “average of
, we will do a pretty good job approximating the integral. So what we end up computing is the “average of
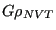 over
over
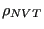 ”:
”:
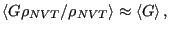 |
(69) |
which should give an excellent approximation for
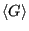 . The idea of using
. The idea of using
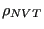 as the sampling distribution is due to Metropolis et al. [3]. This makes the real work in computing
as the sampling distribution is due to Metropolis et al. [3]. This makes the real work in computing
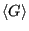 generating states that randomly sample
generating states that randomly sample
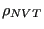 .
.
Metropolis et al. [3] showed that an efficient way to do this involves generating a Markov chain of states which is constructed such that its limiting distribution is
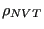 . A Markov chain is just a sequence of trials, where (i) each trial outcome is a member of a finite set and (ii) every trial outcome depends only on the outcome that immediately precedes it. By “limiting distribution,” we mean that the trial acceptance probabilities are tuned such that the probability of observing the Markov chain atop a particular state is defined by some equilibrium probability distribution,
. A Markov chain is just a sequence of trials, where (i) each trial outcome is a member of a finite set and (ii) every trial outcome depends only on the outcome that immediately precedes it. By “limiting distribution,” we mean that the trial acceptance probabilities are tuned such that the probability of observing the Markov chain atop a particular state is defined by some equilibrium probability distribution, 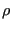 . For the following discussion, it will be convenient to denote a particular state
. For the following discussion, it will be convenient to denote a particular state 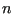 using
using 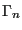 , instead of
, instead of 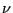 .
.
A trial is some perturbation (usually small) of the coordinates specifying a state. For example, in an Ising system, this might mean flipping a randomly selected spin. In a system of particles in continuous space, it might mean displacing a randomly selected particle by a small amount 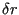 in a randomly chosen direction
in a randomly chosen direction
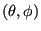 . There can be a large variety of such “trial moves” for any particular system.
. There can be a large variety of such “trial moves” for any particular system.
The probability that a trial move results in a successful transition from state 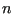 to
to 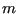 is denoted
is denoted 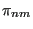 and
and 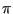 is called the “transition matrix.” It must be specified ahead of time to execute a traditional Markov chain. Since the probability that a trial results in a successful transition to any state, the rows of
is called the “transition matrix.” It must be specified ahead of time to execute a traditional Markov chain. Since the probability that a trial results in a successful transition to any state, the rows of 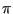 add to unity:
add to unity:
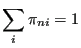 |
(70) |
With this specification, we term 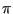 a “stochastic” matrix.
Furthermore, for an equilibrium ensemble of states in state space, we
require that transitions from state to state do not alter state
weights as determined by the limiting distribution. So the weight of
state
a “stochastic” matrix.
Furthermore, for an equilibrium ensemble of states in state space, we
require that transitions from state to state do not alter state
weights as determined by the limiting distribution. So the weight of
state 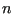 :
:
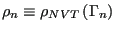 |
(71) |
must be the result of transitions from all other states to state 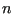 :
:
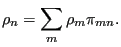 |
(72) |
For all states 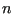 , we can write Eq. 72 as a post-op matrix equation:
, we can write Eq. 72 as a post-op matrix equation:
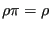 |
(73) |
where 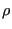 is the row vector of all state weights. Eq. 73 constrains our choice of
is the row vector of all state weights. Eq. 73 constrains our choice of 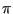 . This means there is still more than one way to specify
. This means there is still more than one way to specify 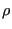 . Metropolis et al. [3] suggested:
. Metropolis et al. [3] suggested:
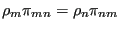 |
(74) |
That is, the probability of transitioning from state 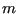 to
to 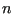 is exactly equal to the probability of transitioning from state
is exactly equal to the probability of transitioning from state 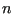 to
to 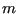 . This is called the “detailed balance” condition, and it guarantees that the state weights remain static. Observe:
. This is called the “detailed balance” condition, and it guarantees that the state weights remain static. Observe:
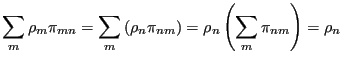 |
(75) |
Detailed balance is, however, overly restrictive; is the only the conceptually simplest way to guarantee that a limiting distribution is obtained. This fact is of little importance in this course, but you may encounter other balance-enforcing conditions in the literature.
Metropolis et al. [3] chose to construct 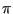 as
as
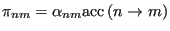 |
(76) |
where 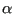 is the probability that a trial move is attempted, and
is the probability that a trial move is attempted, and 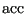 is the probability that a move is accepted. If the probability of proposing a move from
is the probability that a move is accepted. If the probability of proposing a move from 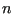 to
to 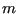 is equal to that of proposing a move from
is equal to that of proposing a move from 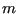 to
to 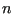 , then
, then
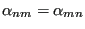 , and the detailed balance condition is written:
, and the detailed balance condition is written:
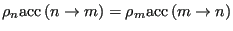 |
(77) |
from which follows
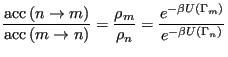 |
(78) |
giving
![$\displaystyle \frac{{\rm acc}\left(n\rightarrow m\right)}{{\rm acc}\left(m\righ...
...eft(\Gamma_n\right)\right]\right\} \equiv \exp\left(-\beta\Delta{U}_{nm}\right)$](img247.png) |
(79) |
where we have defined the change in potential energy as
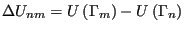 |
(80) |
There are many choices for
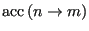 that satisfy Eq. 79. The original choice of Metropolis is used most frequently:
that satisfy Eq. 79. The original choice of Metropolis is used most frequently:
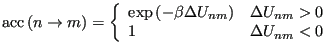 |
(81) |
So, suppose we have some initial configuration 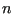 with potential energy
with potential energy 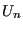 . We make a trial move, temporarily generating a new configuration
. We make a trial move, temporarily generating a new configuration 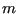 . Now we calculate a new energy,
. Now we calculate a new energy, 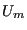 . If this energy is lower than the original, (
. If this energy is lower than the original, (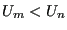 ) we unconditionally accept the move, and configuration
) we unconditionally accept the move, and configuration 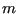 becomes the current configuration. If it is greater than the original, (
becomes the current configuration. If it is greater than the original, (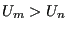 ) we accept it with a probability consistent with the fact that the states both belong to a canonical ensemble. How does one in practice decide whether to accept the move? One first picks a uniform random variate
) we accept it with a probability consistent with the fact that the states both belong to a canonical ensemble. How does one in practice decide whether to accept the move? One first picks a uniform random variate 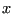 on the interval
on the interval ![$ [0,1]$](img256.png) . If
. If
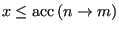 , the move is accepted.
, the move is accepted.
The next section is devoted to an implementation of the Metropolis Monte Carlo method for a 2D Ising magnet.
cfa22@drexel.edu
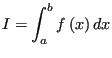
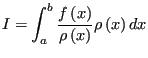
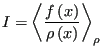
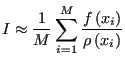
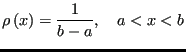
![]() :
:
![]() (Eq. 59) could be discretized using Simpson's rule. If we did that, requesting only a modest 10 discrete points per axis in configurational space, we would need to evaluate the integrand
(Eq. 59) could be discretized using Simpson's rule. If we did that, requesting only a modest 10 discrete points per axis in configurational space, we would need to evaluate the integrand
![]() 10
10![]() times. This is an almost unimaginably large number. Using a direct numerical technique to compute statistical mechanical averages is simply out of the question.
times. This is an almost unimaginably large number. Using a direct numerical technique to compute statistical mechanical averages is simply out of the question.
![]() , such that we minimize the number of points (i.e., the expense) necessary to give an estimate of
, such that we minimize the number of points (i.e., the expense) necessary to give an estimate of
![]() to a given level of accuracy.
to a given level of accuracy.
![]() is large. It stands to reason that if we randomly select points from
is large. It stands to reason that if we randomly select points from
![]() , we will do a pretty good job approximating the integral. So what we end up computing is the “average of
, we will do a pretty good job approximating the integral. So what we end up computing is the “average of
![]() over
over
![]() ”:
”:
![]() . A Markov chain is just a sequence of trials, where (i) each trial outcome is a member of a finite set and (ii) every trial outcome depends only on the outcome that immediately precedes it. By “limiting distribution,” we mean that the trial acceptance probabilities are tuned such that the probability of observing the Markov chain atop a particular state is defined by some equilibrium probability distribution,
. A Markov chain is just a sequence of trials, where (i) each trial outcome is a member of a finite set and (ii) every trial outcome depends only on the outcome that immediately precedes it. By “limiting distribution,” we mean that the trial acceptance probabilities are tuned such that the probability of observing the Markov chain atop a particular state is defined by some equilibrium probability distribution, ![]() . For the following discussion, it will be convenient to denote a particular state
. For the following discussion, it will be convenient to denote a particular state ![]() using
using ![]() , instead of
, instead of ![]() .
.
![]() in a randomly chosen direction
in a randomly chosen direction
![]() . There can be a large variety of such “trial moves” for any particular system.
. There can be a large variety of such “trial moves” for any particular system.
![]() to
to ![]() is denoted
is denoted ![]() and
and ![]() is called the “transition matrix.” It must be specified ahead of time to execute a traditional Markov chain. Since the probability that a trial results in a successful transition to any state, the rows of
is called the “transition matrix.” It must be specified ahead of time to execute a traditional Markov chain. Since the probability that a trial results in a successful transition to any state, the rows of ![]() add to unity:
add to unity:
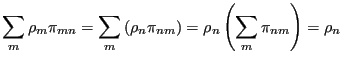
![]() as
as
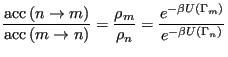
![]() that satisfy Eq. 79. The original choice of Metropolis is used most frequently:
that satisfy Eq. 79. The original choice of Metropolis is used most frequently: