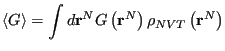Analogous to the quasi-classical microcanonical paritition function of Eq. 6, here is the quasi-classical representation of the canonical partition function:
![$\displaystyle Q_{\rm classical} = \frac{1}{h^{dN}N!}\int \int d{\bf r}^N d{\bf p}^N \exp\left[-\beta\mathscr{H}\left({\bf r}^N,{\bf p}^N\right)\right]$](img180.png) |
(46) |
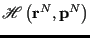 is the Hamiltonian function which computes the energy of a point in phase space. The probability of a point in phase space is represented as
is the Hamiltonian function which computes the energy of a point in phase space. The probability of a point in phase space is represented as
![$\displaystyle P\left({\bf r}^N,{\bf p}^N\right) = \left(Q_{\rm classical}\right)^{-1} \exp\left[-\beta\mathscr{H}\left({\bf r}^N,{\bf p}^N\right)\right].$](img182.png) |
(47) |
So, the general “sum-over-states” ensemble average of quantum statistical mechanics, first presented in Eq. 1, becomes an integral over phase space in classical statistical mechanics:
![$\displaystyle \left<G\right> = \frac{\displaystyle \int \int d{\bf r}^N d{\bf p...
...{\bf p}^N \exp\left[-\beta\mathscr{H}\left({\bf r}^N,{\bf p}^N\right)\right] },$](img183.png) |
(48) |
where
 is the value of the observable
is the value of the observable  at phase space point
at phase space point
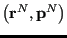 . Before moving on, it is useful to recognize that we normally simplify this ensemble average by noting that, for a system of classical particles, the usual choice for the Hamiltonian has the form
. Before moving on, it is useful to recognize that we normally simplify this ensemble average by noting that, for a system of classical particles, the usual choice for the Hamiltonian has the form
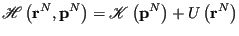 |
(49) |
where
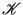 is the kinetic energy, which is only a function of momenta, and
is the kinetic energy, which is only a function of momenta, and 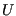 is the potential energy, which is only a function of position. The canonical partition function,
is the potential energy, which is only a function of position. The canonical partition function, 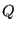 , can in this case be factorized:
, can in this case be factorized:
The quantity in the left-hand braces is the ideal gas partition function, because it corresponds to the case when the potential 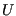 is 0. (Note that we have multiplied and divided by
is 0. (Note that we have multiplied and divided by 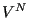 ; this is the equivalent of scaling the positions in the integration over positions.) The quantity in the right-hand braces is called the configurational partition function,
; this is the equivalent of scaling the positions in the integration over positions.) The quantity in the right-hand braces is called the configurational partition function, 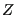 .
.
Because the kinetic energy
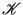 has the simple form,
has the simple form,
 |
(53) |
where  is the mass of particle
is the mass of particle  , the integral over particle momenta can be evaluated analytically:
, the integral over particle momenta can be evaluated analytically:
(We have assumed all particles have the same mass, 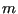 ; in the case
of distinct masses, this is just a product of similar factors.)
; in the case
of distinct masses, this is just a product of similar factors.)
 becomes
becomes
where 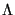 is the de Broglie wavelength, a quantum-mechanical property of a particle inversely proportional to its momentum (and thus inversely proportional to the square root of temperature):
is the de Broglie wavelength, a quantum-mechanical property of a particle inversely proportional to its momentum (and thus inversely proportional to the square root of temperature):
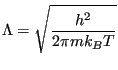 |
(58) |
As an example, for a hydrogen atom with mass 1 amu and at room temperature (298 K),
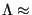 1 Å. The de Broglie wavelength limits the precision by which a particle's position can be determined; for H atoms at room temperature, one is not permitted to specify their positions with a precision finer than about 1 ångstrom without violating the Heisenberg uncertainty principle of quantum mechanics. However, as we will see, in classical molecular simulations, we must lift this restriction, while never forgetting that this makes a classical representation of a molecule somewhat less realistic.
1 Å. The de Broglie wavelength limits the precision by which a particle's position can be determined; for H atoms at room temperature, one is not permitted to specify their positions with a precision finer than about 1 ångstrom without violating the Heisenberg uncertainty principle of quantum mechanics. However, as we will see, in classical molecular simulations, we must lift this restriction, while never forgetting that this makes a classical representation of a molecule somewhat less realistic.
With the momentum degrees of freedom handled at finite temperature, when the observable 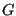 is a function of positions only, the ensemble average becomes a configurational average:
is a function of positions only, the ensemble average becomes a configurational average:
![$\displaystyle \left<G\right> = Z^{-1}\int d{\bf r}^N \exp\left[-\beta U\left({\bf r}^N\right)\right] G\left({\bf r}^N\right).$](img208.png) |
(59) |
Note that the integration over momentum yields a factor
 in both the numerator and denominator, and thus divides out. We can write this configurational average using a probability distribution,
in both the numerator and denominator, and thus divides out. We can write this configurational average using a probability distribution,
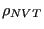 , as
, as
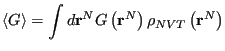 |
(60) |
where
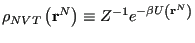 |
(61) |
is called the “canonical probability distribution.” As pointed out on p. 15 of Frenkel & Smit [1], Eq. 59 is “the starting point for virtually all classical simulations of many-body systems”; that is, it is the starting point for almost all simulations discussed in this course.
cfa22@drexel.edu
![]() has the simple form,
has the simple form,
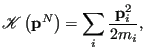
![$\displaystyle \int d{\bf p}^N \exp\left[-\beta\mathscr{K}\left({\bf p}^N\right)\right]$](img197.png)
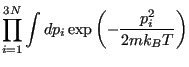
![]() becomes
becomes
![$\displaystyle \frac{V^N}{N!h^{3N}} \int d{\bf p}^N \exp\left[-\beta\mathscr{K}\left({\bf p}^N\right)\right]$](img201.png)
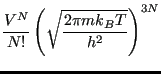
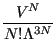
![]() is a function of positions only, the ensemble average becomes a configurational average:
is a function of positions only, the ensemble average becomes a configurational average: