The Code

The complete C program, mdlj.c, contains a complete implementation of the Lennard-Jones force routine and the velocity-Verlet integrator. Compilation instructions appear in the header comments. Let us now consider some sample results from mdlj.c. First, mdlj.c includes an option that outputs a brief summary of the command line options available:

$ mdlj -h
mdlj usage:
mdlj [options]

Options:
         -N [integer]           Number of particles
         -rho [real]            Number density
         -dt [real]             Time step
         -rc [real]             Cutoff radius
         -ns [real]             Number of integration steps
         -T0 [real]             Initial temperature
         -fs [integer]          Sample frequency
         -traj [string]         Trajectory file name
         -prog [integer]        Interval with which logging output is generated
         -icf [string]          Initial configuration file
         -seed [integer]        Random number generator seed
         -uf                    Print unfolded coordinates in trajectory file
         -h                     Print this info

Let us run mdlj.c for 512 particles and 1000 time-steps at a density of 0.85 and an initial temperature of 2.5. We will pick a relatively conservative (small) time-step of 0.001. We will not specify an input configuration, instead allowing the code to create initial positions on a cubic lattice. Here is what we see in the terminal:

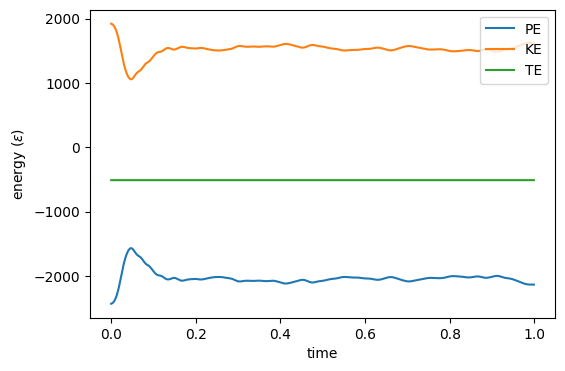
$ ./mdlj -N 512 -fs 10 -ns 1000 -traj traj.xyz -T0 2.5 -rho 0.85 -rc 2.5
# NVE MD Simulation of a Lennard-Jones fluid
# L = 8.44534; rho = 0.85000; N = 512; rc = 2.50000
# nSteps 1000, seed 23410981, dt 0.00100
#LABELS step time PE KE TE drift T P
0 0.00000 -2429.99610 1919.39622 -510.59988  2.58118e-07 2.49921 4.28896
1 0.00100 -2428.18306 1917.58237 -510.60069  1.84111e-06 2.49685 4.30232
2 0.00200 -2425.15191 1914.54975 -510.60216  4.73104e-06 2.49290 4.32466
3 0.00300 -2420.88660 1910.28230 -510.60430  8.92431e-06 2.48735 4.35604
4 0.00400 -2415.36384 1904.75673 -510.60711  1.44276e-05 2.48015 4.39659
5 0.00500 -2408.55314 1897.94254 -510.61060  2.12521e-05 2.47128 4.44649
6 0.00600 -2400.41688 1889.80212 -510.61476  2.94064e-05 2.46068 4.50593
7 0.00700 -2390.91048 1880.29088 -510.61960  3.88852e-05 2.44830 4.57515
8 0.00800 -2379.98339 1869.35814 -510.62525  4.99443e-05 2.43406 4.65427
9 0.00900 -2367.57807 1856.94670 -510.63137  6.19292e-05 2.41790 4.74385
10 0.01000 -2353.63308 1842.99526 -510.63782  7.45638e-05 2.39973 4.84412
11 0.01100 -2338.08390 1827.43905 -510.64484  8.83209e-05 2.37948 4.95492
12 0.01200 -2320.86308 1810.21130 -510.65178  1.01908e-04 2.35705 5.07698
...

Each line of output after the header information corresponds to one time-step. (The header line that begins with the special word #LABELS is used by the Python program plot_mdlj_log.py.) The first column is the time-step, the second is the time value, the third is the potential energy, the fourth is the kinetic energy, the fifth is the total energy, the sixth is the “drift,” the seventh is the instantaneous temperature (Eq. 152), and the eighth is the instantaneous pressure (Eq. 100).

The drift is output to assess the stability of the explicit integration. As a rule of thumb, we would like to keep the drift to below 0.01% of the total energy. The drift reported by mdlj.c is computed as

$$\Delta\mathscr{T}\left(t\right) = \frac{\mathscr{T}\left(t\right)-\mathscr{T}\left(0\right)}{\mathscr{T}\left(0\right)}$$ (154)

where $\mathscr {T}$ is the total energy. The plots below show the output trace for the full 1,000 time-steps. We note that with this time-step value (0.001) keeps the total energy conserved to about one part in 10$^4$.

Figure 14: Left. Potential (PE), kinetic (KE), and total (TE) energies as functions of time in an NVE MD simulation of the Lennard-Jones fluid at reduced temperature $T$ = 2.0. (Initial temperature was set at 2.5.) Right. Drift in total energy (Eq. 154) vs. time.

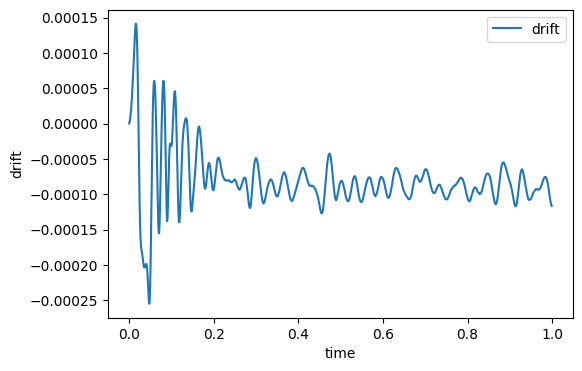Now, this invocation of mdlj.c produces an XYZ-format trajectory file (just like mclj did). Here, I have expanded my XYZ-format convention to allow inclusion of velocities in the output file. Inclusion of velocities is signified by a 1 on the same line as the number of particles (the first line in each frame). If there is a 1 in that position, then each particle line includes three position coordinates and three velocity components:

$ more traj.xyz 
512 1
BOX 8.44534 8.44534 8.44534
16   0.527833   0.527833   0.527833  -0.982352  -0.823300  -1.530590
16   1.583500   0.527833   0.527833  -0.549726  -0.942381   1.363996
16   2.639167   0.527833   0.527833   1.145014  -0.616762  -1.172725
16   3.694834   0.527833   0.527833   1.520337   3.057595  -1.522653
16   4.750501   0.527833   0.527833  -0.541350  -0.144665  -0.919845
16   5.806168   0.527833   0.527833  -0.221483   1.143893  -1.015784
16   6.861835   0.527833   0.527833   5.752205  -1.045603   1.066189
16   7.917502   0.527833   0.527833   0.819532   0.167275  -1.230297
16   0.527833   1.583500   0.527833  -1.062591   2.169692  -1.318921
16   1.583500   1.583500   0.527833  -1.394993   0.055193   1.411530
...

The number “16” at the beginning designates the “type” as an atomic number; for simplicity, I have decided to call all of my particles sulfur. (XYZ format is often used for atomically-specific configurations.) The functions xyz_out() and xyz_in() write and read this format, respectively, in mdlj.c. We will use these functions in other programs as well, typically those which analyze configuration data. Examples of such analysis codes are the subjects of the next two sections.

At this point, you can't do much with all this data, except appreciate just how much data an MD code can produce. In this example, we generated 100 frames of configuration data (positions and velocities) for a 512-atoms system, and the resulting trajectory file is about 3.5 megabytes in size. Of course, that file size scales with both the number of particles and the number of frames it contains. It is not unusual nowadays for researchers to use MD to produce hundreds of gigabytes of configuration data in order to write a single paper. It leads one to think that perhaps a lesson on handling large amounts of data is appropriate for a course on Molecular Simulation; however, I'll forego that for now by trying to keep our sample exercises small.

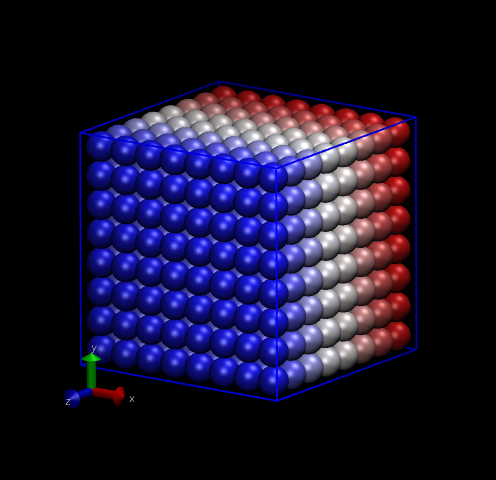
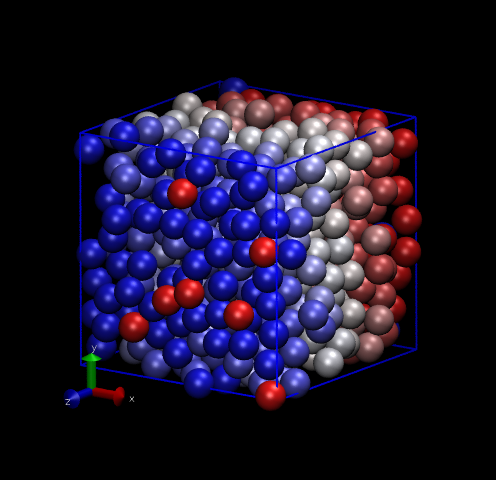
One thing we can do with this data is make nice pictures using VMD. Below are two renderings, one of the initial snapshot, and the other at time $t$ = 1 (1000 time steps). Notice how the initially perfect crystalline lattice has been wiped out.

Figure 15: VMD-generated snapshots of configurations from an NVE MD simulation of the Lennard-Jones fluid at density $\rho$ = 0.85 and average temperature $\left <T\right > \approx 2$. Particles are colored according to their initial $z$ position.