

Next: The Algorithm
Up: Advanced Topics
Previous: Ewald Summation: Suggested Exercises
Densities of States: The Wang-Landau Monte Carlo Method
One of the most interesting recent developments in molecular
simulation are the so-called ``density of states'' methods, first
implemented by Wang and Landau [22,23]. In
principle, these techniques provide a route to calculating the density of states of a system of interest, 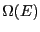 (Eq. 19). 6 Determining
(Eq. 19). 6 Determining 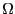 gives a
full understanding of the thermodynamics of a system, because the entropy
is calculable directly as
gives a
full understanding of the thermodynamics of a system, because the entropy
is calculable directly as
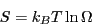 |
(342) |
So, it is not undesirable at all to be able to compute 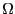 .
.
Now, we know that 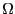 is buried in the probability distribution
of energy that arises from standard NVT Monte Carlo simulation:
is buried in the probability distribution
of energy that arises from standard NVT Monte Carlo simulation:
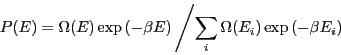 |
(343) |
If we run a simple NVT MC simulation and populate a histogram of total
energy, 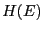 , we can in principle compute
, we can in principle compute 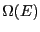 by first
normalizing
by first
normalizing 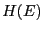
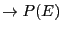 and multiplying each entry
and multiplying each entry 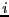 by the factor
by the factor
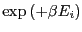 . The problem in practice
is that states for which the Boltzmann factor (
. The problem in practice
is that states for which the Boltzmann factor (
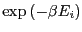 ) is low are rarely if ever visited in reasonable time, and
the statistical strength of
) is low are rarely if ever visited in reasonable time, and
the statistical strength of 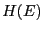 in such regions of energy is
therefore poor. Indeed, conventional MC is designed to not
cover all of energy space, but to perform importance sampling of
configurational space. Furthermore, if the Markov process is trapped
in a local minimum on the potential energy hypersurface, barrier
states with vanishingly small Boltzmann factors effectively prevent
the escape of the process, preventing an adequate sampling of the
potential energy hypersurface. For these reasons, it is desirable to
perform a random walk in energy rather than configurational space.
in such regions of energy is
therefore poor. Indeed, conventional MC is designed to not
cover all of energy space, but to perform importance sampling of
configurational space. Furthermore, if the Markov process is trapped
in a local minimum on the potential energy hypersurface, barrier
states with vanishingly small Boltzmann factors effectively prevent
the escape of the process, preventing an adequate sampling of the
potential energy hypersurface. For these reasons, it is desirable to
perform a random walk in energy rather than configurational space.
In this section, we'll review the two papers by Wang and Landau which
introduced their technique by demonstrating how to compute 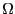 for Ising and Potts systems by conducting random walks in energy
space. These are lattice systems; more recent work has been focused
on developing efficient continuous-space versions of the technique
(E.g., [24,25]).
for Ising and Potts systems by conducting random walks in energy
space. These are lattice systems; more recent work has been focused
on developing efficient continuous-space versions of the technique
(E.g., [24,25]).
Subsections


Next: The Algorithm
Up: Advanced Topics
Previous: Ewald Summation: Suggested Exercises
cfa22@drexel.edu
![]() (Eq. 19). 6 Determining
(Eq. 19). 6 Determining ![]() gives a
full understanding of the thermodynamics of a system, because the entropy
is calculable directly as
gives a
full understanding of the thermodynamics of a system, because the entropy
is calculable directly as
![]() is buried in the probability distribution
of energy that arises from standard NVT Monte Carlo simulation:
is buried in the probability distribution
of energy that arises from standard NVT Monte Carlo simulation:
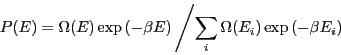
![]() for Ising and Potts systems by conducting random walks in energy
space. These are lattice systems; more recent work has been focused
on developing efficient continuous-space versions of the technique
(E.g., [24,25]).
for Ising and Potts systems by conducting random walks in energy
space. These are lattice systems; more recent work has been focused
on developing efficient continuous-space versions of the technique
(E.g., [24,25]).