The Potts Model treated by Wang-Landau MC

Now we will use the WL algorithm to compute $\Omega (E)$ for the $L$ = 12 ten-state Potts model. (I used the code wl-w.c to obtain these results.) The relevant run parameters we have to specify are the exponent for the update rule of the factor $f$, the initial and final values of $f$, and the flatness criterion for the histogram. The data presented here are from a single run for which $\ln f_{\rm initial}$ = 1, $\ln f_{\rm final}$ = 10$^{-8}$, and $\ln f_{i+1} = \frac{1}{2}\ln f_{i}$; this prescribes a total of 26 independent values of $f$ for which a random walk in energy space must be executed. A histogram is considered sufficiently flat if the minimum value if the histogram is greater than or equal to 80% of the mean value.

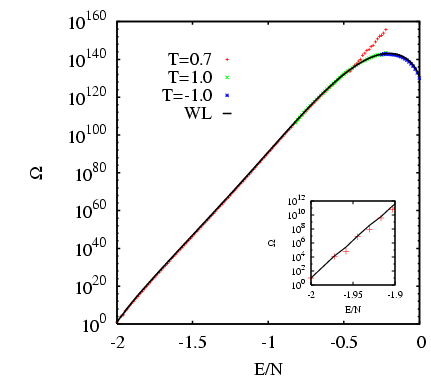
The figure below shows the resulting final $\Omega (E)$, compared to the piecemeal $\Omega (E)$ computed from three NVT MC simulations. We see that the two methods give essentially the same function.

Density of states, $\Omega (E)$, for the $L$ = 12 ten-state Potts model, computed by the WL technique, and pieced together from NVT MC.

The close-up shown in the inset reveals some significant differences at the lowest energy levels between the WL and NVT results. This is because the visits to the lowest energy levels were quite rare in the MC case, making the statistical accuracy of the energy histogram in this subdomain poor.

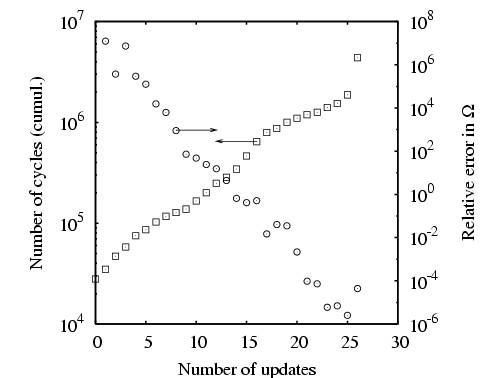
The next figure shows the cumulative cost (in number of cycles) of the WL method for this system, and the relative error in neighboring estimates of $\Omega$, as functions of the number of updates to the factor $f$. The relative error is defined as

$$\epsilon\equiv \int dE \left(\ln\Omega_{i}-\ln\Omega_{i-1}\right)^2$$ (359)

Cumulative number of cycles and relative error vs. $f$-update number in WL sampling of the $L$ = 12 ten-state Potts model.

We see from this data that it requires roughly $10^6$ cycles to converge $\Omega$ to a tolerance of about 10$^{-4}$, and that an additional $3\times 10^6$ cycles does not improve this convergence. So, WL for this system is somewhat less expensive than the $3\times 10^6$ required for the canonical MC runs.

Of course, the canonical MC runs would have been much more expensive had I not known ahead of time what the critical temperature was. For the WL method, no such knowledge is required a priori.

It should be pointed out that $L$ = 12 is a very small system. Wang and Landau broke major new ground in studying the thermodynamics of the Potts model by considering $L$ up to 200.

Although WL does arrive at an accurate estimate of $\Omega$, it is not dramatically more efficient than conventional NVT MC. One of the reasons is due to the nature of the random walk: ``steps'' in energy space are necessarily local. Changing one spin changes energy by at most $\pm$4, and on average the change in energy per flip is much lower in absolute value than that. So the system can spend a lot of time trying to get away from a large subdomain of energy space for which the histogram is already sufficiently flat, in order to explore neighboring subdomains. WL showed that this deficiency can be partially avoided by conducting several parallel runs in different energy windows, which overlap a little bit to allow matching of the resulting densities of states.