

Next: Course Projects
Up: Densities of States: The
Previous: The Potts Model treated
In this section, we report results of a small case study which
investigates the required flatness criterion to achieve a converged
density of states. We will consider the converged 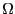 computed
using the 80% criterion as the ``exact'' result, and compare this to
computed
using the 80% criterion as the ``exact'' result, and compare this to
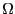 's computed using the criterion that every bin in the energy
histogram has at least
's computed using the criterion that every bin in the energy
histogram has at least 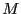 hits. We considered
hits. We considered
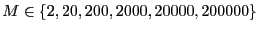 . In order
to minimize the number of cycles, we will sample the histogram (that
is, query its flatness) once per cycle. We also used the same
termination criterion for the update of
. In order
to minimize the number of cycles, we will sample the histogram (that
is, query its flatness) once per cycle. We also used the same
termination criterion for the update of 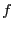 . In the figure below, I
show both the relative error between
. In the figure below, I
show both the relative error between 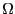 computed with the
computed with the
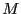 -criterion and
-criterion and
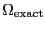 , as well as the number of
cycles required for the
, as well as the number of
cycles required for the 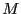 -criterion computation.
-criterion computation.
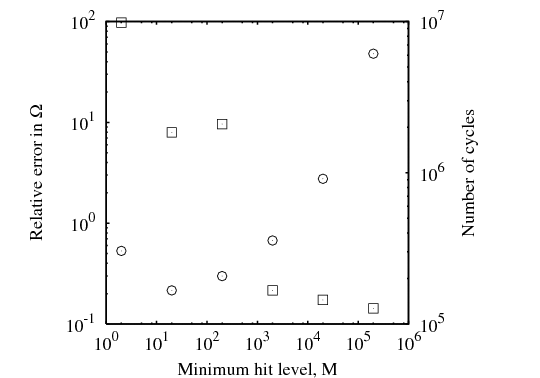 |
Relative error (  ) and number of cycles ( 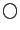 ) vs. minimum hit level 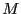 for
flatness in WL sampling of the 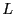 = 12 ten-state Potts model.
|
|
Interestingly, we see that even out to 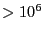 cycles, our result has
only marginally converged to the exact result; an error of
cycles, our result has
only marginally converged to the exact result; an error of 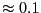 is larger than the iteration-to-iteration convergence tolerance
of
is larger than the iteration-to-iteration convergence tolerance
of
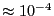 observed in the original run. Nevertheless, this
level of error is very small; the curves are indistinguishable on a plot.
Another interesting fact is that the
observed in the original run. Nevertheless, this
level of error is very small; the curves are indistinguishable on a plot.
Another interesting fact is that the 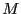 = 2 run is apparently more
expensive than the
= 2 run is apparently more
expensive than the 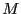 = 20 run. This is likely due to fact that
the initial configuration for each run segment (each value of
= 20 run. This is likely due to fact that
the initial configuration for each run segment (each value of 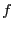 ) is
different; it is the final configuration from the previous segment. It
just so happens that the 23rd iteration for
) is
different; it is the final configuration from the previous segment. It
just so happens that the 23rd iteration for 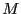 = 2 begins in a configuration
that initiates a walk that more slowly covers energy space than the
configurations in the
= 2 begins in a configuration
that initiates a walk that more slowly covers energy space than the
configurations in the 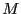 = 20 runs. Beyond
= 20 runs. Beyond 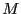 = 20, the behavior
is as expected: increasing
= 20, the behavior
is as expected: increasing 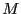 makes the simulation more expensive.
makes the simulation more expensive.


Next: Course Projects
Up: Densities of States: The
Previous: The Potts Model treated
cfa22@drexel.edu
![]() computed
using the 80% criterion as the ``exact'' result, and compare this to
computed
using the 80% criterion as the ``exact'' result, and compare this to
![]() 's computed using the criterion that every bin in the energy
histogram has at least
's computed using the criterion that every bin in the energy
histogram has at least ![]() hits. We considered
hits. We considered
![]() . In order
to minimize the number of cycles, we will sample the histogram (that
is, query its flatness) once per cycle. We also used the same
termination criterion for the update of
. In order
to minimize the number of cycles, we will sample the histogram (that
is, query its flatness) once per cycle. We also used the same
termination criterion for the update of ![]() . In the figure below, I
show both the relative error between
. In the figure below, I
show both the relative error between ![]() computed with the
computed with the
![]() -criterion and
-criterion and
![]() , as well as the number of
cycles required for the
, as well as the number of
cycles required for the ![]() -criterion computation.
-criterion computation.
