Statistical Mechanics: A Brief Introduction

This course is centered upon a mathematical statement called an “ensemble average”:

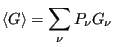$$\left<G\right> = \sum_\nu P_\nu G_\nu$$ (1)

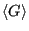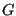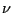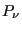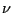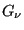That is, the expectation value, $\left<G\right>$, of some observable property $G$ is an average over all possible microstates available to a system, indexed by $\nu$, where $P_\nu$ is the probability of observing the system in microstate $\nu$, and $G_\nu$ is the value of the measured property 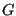$G$ when the system is in microstate 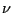$\nu$. Before even considering how to use computer simulation to make such a measurement of a particular property for a particular system, there are three main issues to consider:

1. What is a microstate?
2. What is meant by observing the system?
3. How do we calculate probabilities?

In the following subsections, we give a cursory treatment of elmentary statistical mechanics aimed at answering these questions. The aim is to give the student an appreciation of the basic physics that underlies a majority of current molecular simulation.